背景资料
我们先来看一下某培训机构的一道注册岩土考试的习题:
某当土墙高7m,墙背倾角为$\alpha=60^{\circ}$,墙后填土为砂土$c=0kPa$,$\phi=30^{\circ}$,$\gamma=19kN/m^3$,坡顶倾角$\beta=15^{\circ}$,墙背与土的摩擦角$\delta=10^{\circ}$,问作用于墙背的主动土压力为多少?
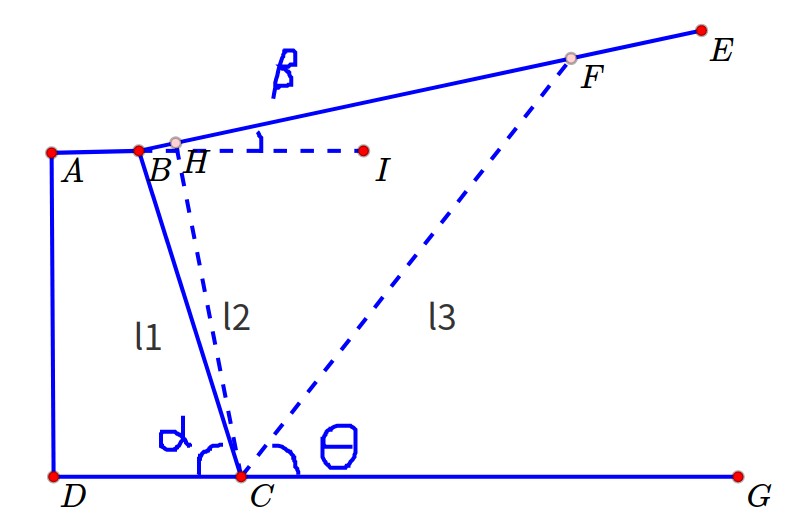
分析
破裂临界角度
$$
\epsilon=45^{\circ}-\frac{30^{\circ}}{2}+\frac{15^{\circ}}{2}-\frac{1}{2}arcsin(\frac{sin15^{\circ}}{sin30^{\circ}})=21.09^{\circ}<90^{\circ}-60^{\circ}=30^{\circ}
$$
暂时以第二破裂面进行计算
$$
l_1=\frac{7}{sin60^{\circ}}=8.083m
$$
$$
l_2=\frac{7sin(60^{\circ}+15^{\circ})}{sin60^{\circ}sin(180^{\circ}-15^{\circ}-68.09^{\circ})}=7.865m
$$
$$
l_3=\frac{7sin(60^{\circ}+15^{\circ})}{sin60^{\circ}sin(\theta-15^{\circ})}=\frac{7.807}{sin(\theta-15^{\circ})}m
$$
假想墙背主动土压力
$$
E_a=\frac{\frac12\times7.865\times\frac{7.807}{sin(\theta-15^{\circ})}\times sin(180^{\circ}-68.09^{\circ}-\theta)\times19\times sin(\theta-30^{\circ})}{sin(\theta-30^{\circ}+68.09^{\circ}-30^{\circ})}
$$
令$\frac{dE_a}{d\theta}=0$,求得$$\theta=51.9^{\circ}$$
此时
$$
E_a=362.43kN/m
$$
水平分力
$$
E_{ax}=362.43\sin(68.09^{\circ}-30^{\circ})=223.58kN/m
$$
竖向分力
$$
E_{ay}=362.43\cos(68.09^{\circ}-30^{\circ})=285.25kN/m
$$
重力
$$
G=\frac12\times8.083\times7.865\times\sin8.09^{\circ}\times19=84.99kN/m
$$
墙背主动土压力
$$
E^{‘}_{a}=\sqrt{223.58^2+(285.25+84.99)^2}=432.51kN/m
$$
某培训机构的解析到此结束。
疑问
其实再往下思考,继续求得此时墙背真正的摩擦角
$$
\delta=\arctan(\frac{233.58}{285.25+84.99})=28.87^{\circ}>10^{\circ}
$$
而墙背能发挥的最大摩擦角为$\delta=10^{\circ}$,并不能提供$28.87^{\circ}$的摩擦角,此时该如何处理?
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 admin@yantu.org